Huffman Text Compression
Concept
Lossless text compression has always been something that I wanted to figure out and play around with, and just the other day I stumbled upon a Tom Scott video centered around the method known as Huffman coding. Huffman coding is perhaps the most signigicant text compression algorithm ever invented, and has been mathematically proven to be the single most space efficient character string compression algorithm possible. It's based on the idea of assigning unique bit signatures to all ascii characters, which are shorter the more often a specific character is used in the text. It seems like a no brainer to just make the things we have a lot of smaller, but it's not necessarily that simple when you consider that computers view text as constant streams of bits, and without consistent character sizes, it becomes tricky to mark after which bit a character ends and another one begins. This is all explained much more effectively in Tom's video.
Data Structures
For the following demonstrations, we will use these structures to hold all necessary data. Huffman encoding is based on binary trees, so we will create nodes that hold: the relevant character (or null), it's frequency, and two children. The tree container will also hold the string to be compressed and a lookup table (LUT) which I will explain later.
struct HuffmanNode
{
std::unique_ptr<HuffmanNode> c1 = nullptr, c2 = nullptr;
char character = '\0';
size_t count = 0;
...
};
class HuffmanTree
{
std::string m_src;
HuffmanNode m_root;
std::unordered_map<char, std::string> m_lut;
...
};
Counting Characters
The first thing to do when constructing our Huffman Tree is to create a list of all characters, aswell as their respective frequencies. Getting the frequency of each character in the string is trivial, and I will not explain it in much detail here. Just know that for later generation of the Huffman Tree, it is useful to already save these frequencies as a vector of Nodes (leaving the children fields of all nodes as 'null').
std::vector<HuffmanNode> counts;
Generating the Huffman Tree
A Huffman Tree is a binary tree where each leaf represents a text character. This results in each leaf having a unique binary representation (being the collection of all 1/0 branch paths you took to reach it) which is not the same as or contained within the representation of any other leaf. As explained above, the more frequent a character is, the less bits a character uses. Thus, frequent characters are placed at close to the root of the tree, where fewer branches have been taken.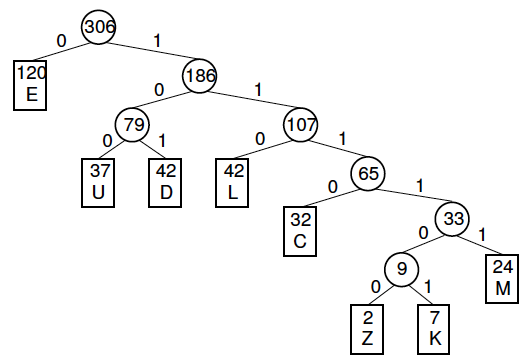
If you have been following so far, great. However I regret to inform you that this is an act I can no longer keep up. Beyond this point, if
you wish to truly understand how this algorithm works, you will have to do with your own research. I can however still explain to you how I
implemented things. The algorithm is as follows:
- Take the trailing 2 elements in your list of character counts, and put them together as the children of a new tree node.
- Define that node's "character count" (though the node represents no character) as the sum of it's children's counts.
- Insert that node back into the list such that the list remains sorted by count.
- Repeat until the list only contains one node. This node is the root of the complete tree.
std::vector<HuffmanNode> counts = getCounts();
HuffmanNode* c1 = new HuffmanNode(std::move(counts[0]));
HuffmanNode* c2 = new HuffmanNode(std::move(counts[1]));
while (counts.size() > 2)
{
counts.erase(counts.begin());
counts.erase(counts.begin());
if (c1->count + c2->count > counts.back().count)
counts.emplace_back('\0', c1->count + c2->count, c1, c2);
else
{
for (auto it = counts.begin(); it != counts.end(); it++)
{
if (c1->count + c2->count <= it->count)
{
counts.emplace(it, '\0', c1->count + c2->count, c1, c2);
break;
}
}
}
c1 = new HuffmanNode(std::move(counts[0]));
c2 = new HuffmanNode(std::move(counts[1]));
}
m_root = HuffmanNode{ '\0', c1->count + c2->count, c1, c2 };
Creating a Lookup Table
For efficiency when later converting each character to bits, we will deviate from the standard algorithm slightly to create a lookup table. This LUT will map each character to it's own bit-sequence. To do this, we define a recursive function to traverse down the tree, tracking it's position (bit-sequence) as it goes. When it reaches a node with a valid character, we know we have reached a leaf, and we can save into the LUT the character and it's corresponding bit-sequence for quick and easy retrieval later on.
void HuffmanTree::generateLUT(const HuffmanTree::HuffmanNode& n, std::string pos = "")
{
if (n.c1->character != '\0')
m_lut[n.c1->character] = pos + "0";
else
recurseLUT(*n.c1, pos + "0");
if (n.c2->character != '\0')
m_lut[n.c2->character] = pos + "1";
else
recurseLUT(*n.c2, pos + "1");
}
Performing the Compression
We're almost there. All that remains to be done is to cycle through all characters in our given string, retrieve the corresponding bits from the LUT and output them to some kind of output stream. This is however only slightly easier said than done. The tricky thing is that stream objects (primarily file streams) in most languages prefer to recieve their data in blocks of 8 bits, and we've just tried our absolute hardest to leave said 8-bit world. We can however get around this with a bit of buffering and some bitwise magic. We must first define an 8-bit buffer (unsigned char) and a counter for how many bits the character currently stores. Then, as we go through our characters, for each bit in that characters sequence, we add 1 to the buffer if the bit is 1, bitshift the entire buffer to the left, and increment the buffer size counter. Effectively, we are now writing individual bits from left to right. all that remains to be done is to output the buffer and reset it every time our buffer size counter reaches 8, or we will overflow.
void HuffmanTree::compress(std::ostream& stream)
{
uint8_t buffer = 0;
int buflen = 0;
for (const char c : (m_src + "zzz"))
{
const std::string code = m_lut.at(c);
for (const char d : code)
{
buffer = buffer << 1;
buffer += static_cast<uint8_t>(d == '1');
buflen++;
if (buflen == 8)
{
stream.write((char*)&buffer, sizeof(uint8_t));
buflen = 0;
buffer = 0;
}
}
}
}
void HuffmanTree::decompress(std::istream& stream)
{
uint8_t buffer;
stream.read((char*)&buffer, sizeof(uint8_t));
int buflen = 8;
while (!stream.eof())
{
const HuffmanNode* n = &m_root;
char c = '\0';
while (c == '\0')
{
if (buffer & 128)
n = n->c2.get();
else
n = n->c1.get();
c = n->character;
buffer = buffer << 1;
buflen--;
if (buflen == 0)
{
stream.read((char*)&buffer, sizeof(uint8_t));
buflen = 8;
}
}
m_src += c;
}
for (size_t i = 0; i < 3; i++)
m_src.pop_back();
}
Hold Up
std::vector<HuffmanNode> HuffmanTree::getCounts(std::istream& stream)
{
std::vector<HuffmanNode> result;
while (true)
{
char character = '\0';
stream.read((char*)&character, sizeof(char));
if (character == '\0')
return result;
size_t count = 0;
stream.read((char*)&count, sizeof(size_t));
result.emplace_back(character, count, nullptr, nullptr);
}
return result;
}
void HuffmanTree::dumpCounts(std::ostream& stream)
{
std::vector<HuffmanNode> counts = getSortedChars(m_src.c_str());
for (const auto& c : counts)
{
stream.write(&c.character, sizeof(char));
stream.write((char*)&c.count, sizeof(size_t));
}
char endoflist = '\0';
stream.write(&endoflist, sizeof(char));
}